- Twierdzenie o czworokącie opisanym na okręgu: link
- Twierdzenie o czworokącie wpisanym w okrąg: link
- Przykładowe zadania:
Zadanie nr 1. (Matura maj 2018, poziom rozszerzony)
Trójkąt 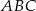 jest ostrokątny oraz
jest ostrokątny oraz 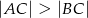 . Dwusieczna
. Dwusieczna 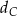 kąta
kąta 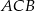 przecina bok
przecina bok 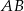 w punkcie
w punkcie 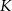 . Punkt
. Punkt 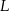 jest obrazem punktu
jest obrazem punktu 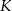 w symetrii osiowej względem dwusiecznej
w symetrii osiowej względem dwusiecznej 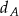 kąta
kąta 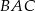 , punkt
, punkt 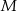 jest obrazem punktu
jest obrazem punktu 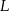 w symetrii osiowej względem dwusiecznej
w symetrii osiowej względem dwusiecznej 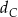 kąta
kąta 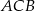 , a punkt
, a punkt 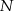 jest obrazem punktu
jest obrazem punktu 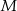 w symetrii osiowej względem dwusiecznej
w symetrii osiowej względem dwusiecznej 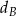 kąta
kąta 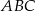 (zobacz rysunek).
(zobacz rysunek).
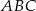 jest ostrokątny oraz
jest ostrokątny oraz 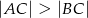 . Dwusieczna
. Dwusieczna 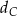 kąta
kąta 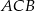 przecina bok
przecina bok 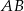 w punkcie
w punkcie 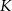 . Punkt
. Punkt 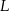 jest obrazem punktu
jest obrazem punktu 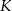 w symetrii osiowej względem dwusiecznej
w symetrii osiowej względem dwusiecznej 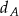 kąta
kąta 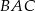 , punkt
, punkt 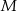 jest obrazem punktu
jest obrazem punktu 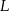 w symetrii osiowej względem dwusiecznej
w symetrii osiowej względem dwusiecznej 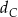 kąta
kąta 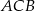 , a punkt
, a punkt 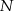 jest obrazem punktu
jest obrazem punktu 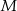 w symetrii osiowej względem dwusiecznej
w symetrii osiowej względem dwusiecznej 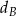 kąta
kąta 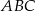 (zobacz rysunek).
(zobacz rysunek). 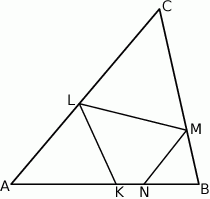
Udowodnij, że na czworokącie 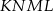 można opisać okrąg.
można opisać okrąg.
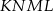 można opisać okrąg.
można opisać okrąg.
Zadanie nr 2. (Matura maj 2018, poziom rozszerzony)
Rozpatrujemy wszystkie trapezy równoramienne, w które można wpisać okrąg, spełniające warunek: suma długości dłuższej podstawy  i wysokości trapezu jest równa 2.
i wysokości trapezu jest równa 2.
 i wysokości trapezu jest równa 2.
i wysokości trapezu jest równa 2. - Wyznacz wszystkie wartości
 , dla których istnieje trapez o podanych własnościach.
, dla których istnieje trapez o podanych własnościach. - Wykaż, że obwód
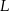 takiego trapezu, jako funkcja długości
takiego trapezu, jako funkcja długości  dłuższej podstawy trapezu, wyraża się wzorem
dłuższej podstawy trapezu, wyraża się wzorem 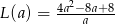
Zadanie nr 3. (Matura czerwiec 2018, poziom rozszerzony)
Trapez prostokątny 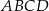 o podstawach
o podstawach 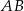 i
i 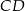 jest opisany na okręgu. Ramię
jest opisany na okręgu. Ramię 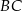 ma długość 10, a ramię
ma długość 10, a ramię 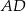 jest wysokością trapezu. Podstawa
jest wysokością trapezu. Podstawa 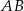 jest 2 razy dłuższa od podstawy
jest 2 razy dłuższa od podstawy 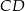 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
Zadanie nr 4. (Matura czerwiec 2017, poziom rozszerzony)
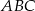 są równe
są równe 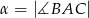 ,
, 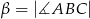 i
i 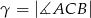 . Punkt
. Punkt 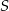 jest środkiem okręgu wpisanego w ten trójkąt, a proste zawierające odcinki
jest środkiem okręgu wpisanego w ten trójkąt, a proste zawierające odcinki 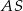 i
i 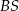 przecinają boki
przecinają boki 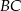 i
i 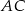 tego trójkąta w punktach odpowiednio
tego trójkąta w punktach odpowiednio 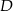 i
i 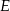 (zobacz rysunek).
(zobacz rysunek). 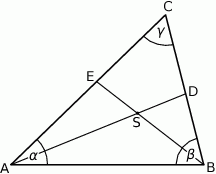
Wykaż, że jeżeli 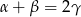 , to na czworokącie
, to na czworokącie 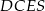 można opisać okrąg.
można opisać okrąg.
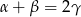 , to na czworokącie
, to na czworokącie 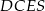 można opisać okrąg.
można opisać okrąg.
Zadanie nr 5. (Matura czerwiec 2017, poziom rozszerzony)
Trapez równoramienny 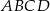 o ramieniu długości 6 wpisany jest w okrąg, przy czym dłuższa podstawa
o ramieniu długości 6 wpisany jest w okrąg, przy czym dłuższa podstawa 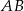 trapezu, o długości 12, jest średnicą tego okręgu. Przekątne
trapezu, o długości 12, jest średnicą tego okręgu. Przekątne 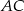 i
i 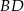 trapezu przecinają się w punkcie
trapezu przecinają się w punkcie 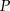 . Oblicz pole koła wpisanego w trójkąt
. Oblicz pole koła wpisanego w trójkąt 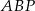 .
.
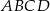 o ramieniu długości 6 wpisany jest w okrąg, przy czym dłuższa podstawa
o ramieniu długości 6 wpisany jest w okrąg, przy czym dłuższa podstawa 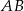 trapezu, o długości 12, jest średnicą tego okręgu. Przekątne
trapezu, o długości 12, jest średnicą tego okręgu. Przekątne 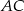 i
i 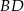 trapezu przecinają się w punkcie
trapezu przecinają się w punkcie 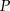 . Oblicz pole koła wpisanego w trójkąt
. Oblicz pole koła wpisanego w trójkąt 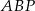 .
.
Rozwiązania zadań
(uczyłam się pisać na tablecie, pozostało Wam tylko zadanie nr 1 - proste)
Brak komentarzy:
Prześlij komentarz