16.03.2020
DODATKOWE ZADANIA
17.03.2020
Ciekawe zadanie 4.29 dla ambitnych (zastosuj np tw. cosinusów),
4.30 dla wszystkich (odp. 620, dane: a3*a5=20, a17:a5=2 reszta 1, oblicz sumę od a20 do a50 włącznie)
Zadania do samodzielnego rozwiązania
proszę o rozwiązanie i sprawdzenie poprawności (rozwiązania - ok. godz. 12.00, 17.03.20)
18.03.2020
zadania na dziś, miłej pracy :)
Zadanie 1.
Pierwiastkami wielomianu W(x) = x3 + px2 + 23x + q są trzy liczby tworzące ciąg arytmetyczny. Wiedząc, że suma pierwiastków wielomianu jest równa 9, oblicz wartości parametrów p i q oraz pierwiastki wielomianu W(x).
Zadanie 2.
Wyznacz wszystkie wartości x i y, dla których ciąg (x – y2, –y – x2, x – 2y – 3) jest jednocześnie arytmetyczny i geometryczny.
Zadanie 3.
Pewien ciąg geometryczny (an) ma parzystą liczbę wyrazów. Suma wszystkich wyrazów jest sześć razy większa od sumy wyrazów ciągu stojących na miejscach nieparzystych. Wyznacz iloraz tego ciągu.
Zadanie 4.
Ciąg (an) jest ciągiem geometrycznym o dodatnich wyrazach, a ciąg (bn) – ciągiem arytmetycznym. Pierwsze i piąte wyrazy tych ciągów są równe. Wiedząc, że a1=2, suma dziesięciu początkowych wyrazów ciągu arytmetycznego jest równa 1820, oblicz szósty wyraz ciągu geometrycznego.
19.03.2020
1. PROCENT SKŁADANY
2. Testy do sprawdzenia swojej wiedzy (ciągi-podstawy, ciąg arytmetyczny, ciąg geometryczny)
link: testy
20.03.2020
Typowe zadania z ciągów "pomieszanych":
I TYP - mamy kolejne wyrazy pewnego ciągu i zmieniamy je (dodając/odejmując/mnożąc/dzieląc) na trzy kolejne wyrazy drugiego ciągu
-stosujemy zależności między trzema kolejnymi wyrazami ciągów-arytmetycznym i geometrycznym
Trzy liczby są kolejnymi wyrazami ciągu arytmetycznego. Ich suma wynosi 18. Jeśli największą z tych liczb zwiększymy o 8, a pozostałych nie zmienimy, to uzyskamy trzy kolejne wyrazy ciągu geometrycznego. Wyznacz te liczby.
Wskazówka-tworzymy układ trzech równań z trzema niewiadomymi i z zależności pomiędzy trzema kolejnymi wyrazami ciągu arytmetycznego a+c=2b wstawiamy do równania na sumę - otrzymamy równanie z jedną niewiadomą (b)!
ROZWIĄZANIE
Szukamy trzech liczb 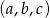 tworzących ciąg arytmetyczny. Ponieważ w takiej sytuacji ciąg
tworzących ciąg arytmetyczny. Ponieważ w takiej sytuacji ciąg 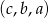 też jest arytmetyczny, możemy założyć (na użytek rachunków), że
też jest arytmetyczny, możemy założyć (na użytek rachunków), że 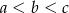 (jeżeli tak nie jest, zapisujemy ciąg w odwrotnej kolejności). Liczby
(jeżeli tak nie jest, zapisujemy ciąg w odwrotnej kolejności). Liczby 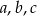 mają spełniać układ równań
mają spełniać układ równań
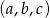 tworzących ciąg arytmetyczny. Ponieważ w takiej sytuacji ciąg
tworzących ciąg arytmetyczny. Ponieważ w takiej sytuacji ciąg 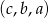 też jest arytmetyczny, możemy założyć (na użytek rachunków), że
też jest arytmetyczny, możemy założyć (na użytek rachunków), że 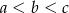 (jeżeli tak nie jest, zapisujemy ciąg w odwrotnej kolejności). Liczby
(jeżeli tak nie jest, zapisujemy ciąg w odwrotnej kolejności). Liczby 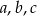 mają spełniać układ równań
mają spełniać układ równań 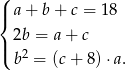
Z pierwszych dwóch równań mamy
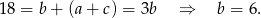
W takim razie
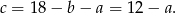
Podstawiamy uzyskane wartości do trzeciego równania i mamy
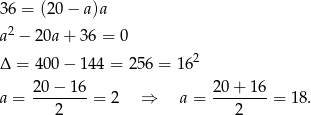
Ponieważ założyliśmy, że 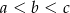 , drugie rozwiązanie odpada i mamy
, drugie rozwiązanie odpada i mamy 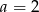 . Wtedy
. Wtedy 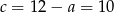 . Pomijając złożenie
. Pomijając złożenie 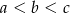 otrzymujemy drugi ciąg spełniający warunki zadania:
otrzymujemy drugi ciąg spełniający warunki zadania: 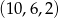 .
.
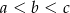 , drugie rozwiązanie odpada i mamy
, drugie rozwiązanie odpada i mamy 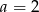 . Wtedy
. Wtedy 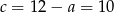 . Pomijając złożenie
. Pomijając złożenie 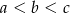 otrzymujemy drugi ciąg spełniający warunki zadania:
otrzymujemy drugi ciąg spełniający warunki zadania: 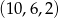 .
.
Odpowiedź: 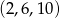 lub
lub 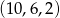
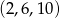 lub
lub 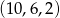
Uwaga-rozwiązanie skopiowałam ze strony zadania.info
jest tam również inny sposób rozwiązania - poszukajcie :)
II TYP - mamy kolejne wyrazy pewnego ciągu i są one wybranymi wyrazami innego ciągu (niekolejnymi-np. pierwszym, drugim i siódmym)
-stosujemy wzór na n-ty wyraz ciągu, z którego wybieramy te "niekolejne wyrazy" i wstawiamy układu (suma podanych wyrazów+zależność na trzy kolejne wyrazy drugiego ciągu)
ROZWIĄZANIE
Z podanej informacji o sumie i o ciągu geometrycznym mamy układ równań.
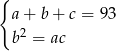
Dodatkowo mamy informację o ciągu arytmetycznym, z której otrzymujemy 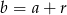 i
i 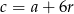 . Mamy więc równania
. Mamy więc równania
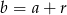 i
i 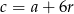 . Mamy więc równania
. Mamy więc równania 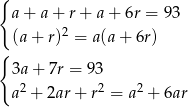
Przekształćmy drugie równanie
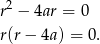
Jeżeli 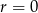 to mamy
to mamy 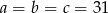 . Jeżeli natomiast
. Jeżeli natomiast 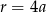 to z pierwszego równania mamy
to z pierwszego równania mamy
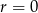 to mamy
to mamy 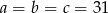 . Jeżeli natomiast
. Jeżeli natomiast 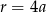 to z pierwszego równania mamy
to z pierwszego równania mamy 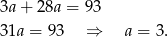
Wtedy 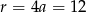 ,
, 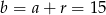 i
i 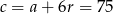 .
.
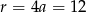 ,
, 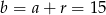 i
i 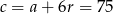 .
. 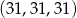 lub
lub 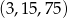
21-22.03.2020
MIŁEGO ODPOCZYNKU!
MIŁEGO ODPOCZYNKU!
Pozdrawiam serdecznie
J Mackiewicz
Od przyszłego tygodnia będę publikować materiały w kolejnych postach.
Od przyszłego tygodnia będę publikować materiały w kolejnych postach.







Brak komentarzy:
Prześlij komentarz