Materiał pochodzi ze strony www.medianauka.pl
Szereg geometryczny
S1 = a1
S2 = a1 + a2
S3 = a1 + a2 + a3
S4 = a1 + a2 + a3 + a4
...
Sn = a1 + a2 + a3 + ... + an
...
S2 = a1 + a2
S3 = a1 + a2 + a3
S4 = a1 + a2 + a3 + a4
...
Sn = a1 + a2 + a3 + ... + an
...
Widzimy, że n-ty wyraz stanowi sumę n kolejnych wyrazów ciągu (an ) począwszy od wyrazu pierwszego.
Ciąg (Sn ) nazywamy szeregiem geometrycznym lub ciągiem sum częściowych ciągu geometrycznego.
Ponieważ n-ty wyraz ciągu geometrycznego wyraża się wzorem 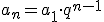 , to szereg geometryczny będzie miał następującą postać:
, to szereg geometryczny będzie miał następującą postać:
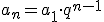 , to szereg geometryczny będzie miał następującą postać:
, to szereg geometryczny będzie miał następującą postać: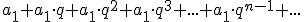
Suma szeregu geometrycznego=suma nieskończonego ciągu geometrycznego
Szereg geometryczny jest zbieżny (istnieje suma nieskończonego ciągu geometrycznego), gdy
|q|<1 (warunek zbieżności szeregu) i ma sumę
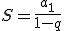
natomiast jest rozbieżny, gdy 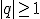
Skąd wziął się powyższy wzór? Ogólny wyraz szeregu geometrycznego to 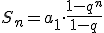 Zatem suma szeregu geometrycznego to granica:
Zatem suma szeregu geometrycznego to granica:
![S=\lim_{n\to\infty}S_n=\lim_{n\to\infty}(a_1\cdot \frac{1-q^n}{1-q})=\lim_{n\to\infty}[\frac{a_1}{1-q}\cdot (1-q^n)]=\\=\lim_{n\to\infty}(\frac{a_1}{1-q}-\frac{a_1}{1-q}q^n)=\frac{a_1}{1-q}-\frac{a_1}{1-q}\cdot{\lim_{n\to\infty}(q^n)}=\frac{a_1}{1-q}-0=\frac{a_1}{1-q}](https://www.medianauka.pl/matematyka/wzory/315/4.gif)
Założyliśmy tutaj, że |q|<1, gdyż tylko wtedy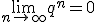 W przeciwnym przypadku granica ta jest nieskończona (niewłaściwa) i suma szeregu również jest nieskończona.
W przeciwnym przypadku granica ta jest nieskończona (niewłaściwa) i suma szeregu również jest nieskończona.
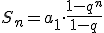 Zatem suma szeregu geometrycznego to granica:
Zatem suma szeregu geometrycznego to granica:![S=\lim_{n\to\infty}S_n=\lim_{n\to\infty}(a_1\cdot \frac{1-q^n}{1-q})=\lim_{n\to\infty}[\frac{a_1}{1-q}\cdot (1-q^n)]=\\=\lim_{n\to\infty}(\frac{a_1}{1-q}-\frac{a_1}{1-q}q^n)=\frac{a_1}{1-q}-\frac{a_1}{1-q}\cdot{\lim_{n\to\infty}(q^n)}=\frac{a_1}{1-q}-0=\frac{a_1}{1-q}](https://www.medianauka.pl/matematyka/wzory/315/4.gif)
Założyliśmy tutaj, że |q|<1, gdyż tylko wtedy
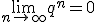 W przeciwnym przypadku granica ta jest nieskończona (niewłaściwa) i suma szeregu również jest nieskończona.
W przeciwnym przypadku granica ta jest nieskończona (niewłaściwa) i suma szeregu również jest nieskończona.Przykładowe zadania wraz z rozwiązaniami (ze strony www.zadania.info i www.medianauka.pl):
Zadanie 1. Wyznacz te wartości  , dla których istnieje suma nieskończonego ciągu geometrycznego
, dla których istnieje suma nieskończonego ciągu geometrycznego
 , dla których istnieje suma nieskończonego ciągu geometrycznego
, dla których istnieje suma nieskończonego ciągu geometrycznego 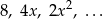
Rozwiązanie:
Będziemy korzystać z faktu, że szereg geometryczny
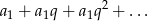
jest zbieżny wtedy i tylko wtedy gdy 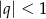 .
.
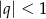 .
.
Iloraz danego ciągu geometrycznego wynosi 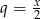 . Musimy zatem rozwiązać nierówność
. Musimy zatem rozwiązać nierówność
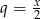 . Musimy zatem rozwiązać nierówność
. Musimy zatem rozwiązać nierówność 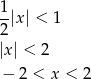
Odpowiedź:
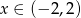
Zadanie 2. Rozwiąż równanie

Rozwiązanie:
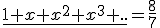
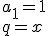
Warunek zbieżności szeregu geometrycznego: |q|=|x|<1.
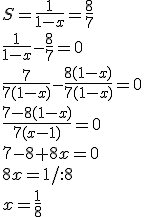
Ponieważ
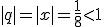 więc x=1/8 jest rozwiązaniem równania.
więc x=1/8 jest rozwiązaniem równania.
Zadania do samodzielnego wykonania:
1. Rozwiąż równanie
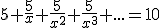
2. Dla jakich wartości parametru x istnieje poniższa suma (jest ona liczbą rzeczywistą)?
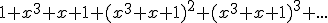
3. Oblicz 10 granic ciągów liczbowych (zadania z zbioru zadań, przykład a)
Brak komentarzy:
Prześlij komentarz