Zadania z szeregu geometrycznego c. d.
wtorek, 31 marca 2020
31.03.2020-zadania z szeregu geometrycznego
Zadania z sumą nieskończonego ciągu geometrycznego
Dodatek do pracy domowej z granic ciągów
Tu można poćwiczyć obliczanie granic ciągów liczbowych
(niestety dość prosty test na stronie e-podręczniki):
poniedziałek, 30 marca 2020
31.03.2020-suma nieskończonego ciągu geometrycznego
Materiał pochodzi ze strony www.medianauka.pl
Szereg geometryczny
S1 = a1
S2 = a1 + a2
S3 = a1 + a2 + a3
S4 = a1 + a2 + a3 + a4
...
Sn = a1 + a2 + a3 + ... + an
...
S2 = a1 + a2
S3 = a1 + a2 + a3
S4 = a1 + a2 + a3 + a4
...
Sn = a1 + a2 + a3 + ... + an
...
Widzimy, że n-ty wyraz stanowi sumę n kolejnych wyrazów ciągu (an ) począwszy od wyrazu pierwszego.
Ciąg (Sn ) nazywamy szeregiem geometrycznym lub ciągiem sum częściowych ciągu geometrycznego.
Ponieważ n-ty wyraz ciągu geometrycznego wyraża się wzorem 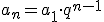 , to szereg geometryczny będzie miał następującą postać:
, to szereg geometryczny będzie miał następującą postać:
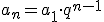 , to szereg geometryczny będzie miał następującą postać:
, to szereg geometryczny będzie miał następującą postać: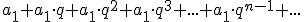
Suma szeregu geometrycznego=suma nieskończonego ciągu geometrycznego
Szereg geometryczny jest zbieżny (istnieje suma nieskończonego ciągu geometrycznego), gdy
|q|<1 (warunek zbieżności szeregu) i ma sumę
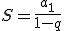
natomiast jest rozbieżny, gdy 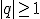
Skąd wziął się powyższy wzór? Ogólny wyraz szeregu geometrycznego to 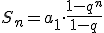 Zatem suma szeregu geometrycznego to granica:
Zatem suma szeregu geometrycznego to granica:
![S=\lim_{n\to\infty}S_n=\lim_{n\to\infty}(a_1\cdot \frac{1-q^n}{1-q})=\lim_{n\to\infty}[\frac{a_1}{1-q}\cdot (1-q^n)]=\\=\lim_{n\to\infty}(\frac{a_1}{1-q}-\frac{a_1}{1-q}q^n)=\frac{a_1}{1-q}-\frac{a_1}{1-q}\cdot{\lim_{n\to\infty}(q^n)}=\frac{a_1}{1-q}-0=\frac{a_1}{1-q}](https://www.medianauka.pl/matematyka/wzory/315/4.gif)
Założyliśmy tutaj, że |q|<1, gdyż tylko wtedy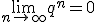 W przeciwnym przypadku granica ta jest nieskończona (niewłaściwa) i suma szeregu również jest nieskończona.
W przeciwnym przypadku granica ta jest nieskończona (niewłaściwa) i suma szeregu również jest nieskończona.
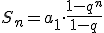 Zatem suma szeregu geometrycznego to granica:
Zatem suma szeregu geometrycznego to granica:![S=\lim_{n\to\infty}S_n=\lim_{n\to\infty}(a_1\cdot \frac{1-q^n}{1-q})=\lim_{n\to\infty}[\frac{a_1}{1-q}\cdot (1-q^n)]=\\=\lim_{n\to\infty}(\frac{a_1}{1-q}-\frac{a_1}{1-q}q^n)=\frac{a_1}{1-q}-\frac{a_1}{1-q}\cdot{\lim_{n\to\infty}(q^n)}=\frac{a_1}{1-q}-0=\frac{a_1}{1-q}](https://www.medianauka.pl/matematyka/wzory/315/4.gif)
Założyliśmy tutaj, że |q|<1, gdyż tylko wtedy
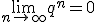 W przeciwnym przypadku granica ta jest nieskończona (niewłaściwa) i suma szeregu również jest nieskończona.
W przeciwnym przypadku granica ta jest nieskończona (niewłaściwa) i suma szeregu również jest nieskończona.Przykładowe zadania wraz z rozwiązaniami (ze strony www.zadania.info i www.medianauka.pl):
Zadanie 1. Wyznacz te wartości  , dla których istnieje suma nieskończonego ciągu geometrycznego
, dla których istnieje suma nieskończonego ciągu geometrycznego
 , dla których istnieje suma nieskończonego ciągu geometrycznego
, dla których istnieje suma nieskończonego ciągu geometrycznego 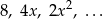
Rozwiązanie:
Będziemy korzystać z faktu, że szereg geometryczny
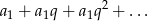
jest zbieżny wtedy i tylko wtedy gdy 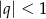 .
.
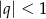 .
.
Iloraz danego ciągu geometrycznego wynosi 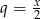 . Musimy zatem rozwiązać nierówność
. Musimy zatem rozwiązać nierówność
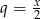 . Musimy zatem rozwiązać nierówność
. Musimy zatem rozwiązać nierówność 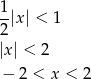
Odpowiedź:
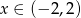
Zadanie 2. Rozwiąż równanie

Rozwiązanie:
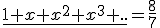
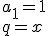
Warunek zbieżności szeregu geometrycznego: |q|=|x|<1.
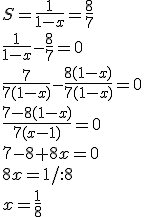
Ponieważ
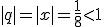 więc x=1/8 jest rozwiązaniem równania.
więc x=1/8 jest rozwiązaniem równania.
Zadania do samodzielnego wykonania:
1. Rozwiąż równanie
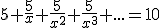
2. Dla jakich wartości parametru x istnieje poniższa suma (jest ona liczbą rzeczywistą)?
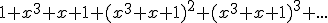
3. Oblicz 10 granic ciągów liczbowych (zadania z zbioru zadań, przykład a)
niedziela, 29 marca 2020
30.03.2020-granice funkcji c.d.
Bardzo proszę o obejrzenie filmu
"Obliczanie granic przez bezpośrednie podstawianie"
i wykonanie zadania
"Obliczane granicy przez bezpośrednie podstawienie"
(w nazwie jest literówka-powinno być Obliczanie, podaję oryginalną nazwę)
Ostateczny termin wykonania: 03.04.2020
piątek, 27 marca 2020
27.03.2020-granice funkcji c.d.
Poproszę o zapoznanie się z materiałami edukacyjnym pt "Formalna definicja granic funkcji"
i wykonanie testu swojej wiedzy
"Podstawy obliczania granic"
Ostateczny termin wykonania: 03.04.2020
czwartek, 26 marca 2020
26.03.2020-granice jednostronne
Proszę o obejrzenie materiałów dotyczących granic jednostronnych funkcji
i wykonanie ćwiczenia
"Jednostronne granice z wykresów"
Ostateczny termin wykonania pracy: 03.04.2020
środa, 25 marca 2020
25.03.2020 - granice funkcji
Polecam cały cykl wykładów on-line na platformie KhanAcademy
szczególnie ciekawy jest temat
Proszę obejrzeć załączone filmy i wykonać ćwiczenie
Szacowanie wartości granic na podstawie wykresów
Ostateczny termin wykonania: 03.04.2020
poniedziałek, 23 marca 2020
Granice ciągów liczbowych - 23-24.03.2020
1. Granice ciągów liczbowych obliczamy przy n dążącym do + nieskończoności (dlaczego?)
2. Bardzo ważne są symbole nieoznaczone, generalnie chodzi o to, żeby je zlikwidować, dlatego wyłączamy n w najwyższej potędze przed nawias
3. Pamiętajmy, że jeśli granice ciągów są właściwe (wartości liczbowe), to nie ma potrzeby sprowadzać sumy czy różnicy wyrażeń wymiernych do wspólnych mianowników (zakazu nie ma, jeżeli ktoś ma pierwiastek masochistyczny)
Przykłady:
4. Dla ciekawych, więcej można poczytać link
2. Bardzo ważne są symbole nieoznaczone, generalnie chodzi o to, żeby je zlikwidować, dlatego wyłączamy n w najwyższej potędze przed nawias
 |
| Materiał ze strony: "e-trapez" |
Przykłady:
Subskrybuj:
Komentarze (Atom)







